lookijumbo.blogg.se - Which composition of similarity transformations maps

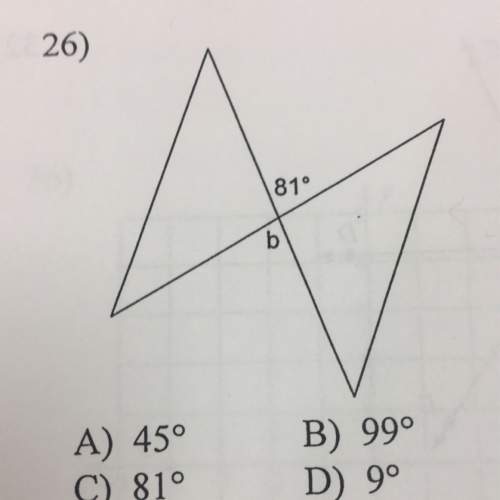
Symbolically, we write the similarity and dissimilarity of two triangles △ ABC and △ A′B′C′ as follows: A B C ∼ A ′ B ′ C ′ īelow the title on the right, the second image shows a similarity decomposed into a rotation and a homothety. Similarity and rotation have the same angle of +135 degrees modulo 360 degrees. The "SAS" is a mnemonic: each one of the two S's refers to a "side" the A refers to an "angle" between the two sides. Which composition of similarity transformations maps polygon ABCD to polygon ABCD a dilation with a scale factor of and. This is known as the SAS similarity criterion. Which transformation maps the large triangle onto the small Which type of triangle will always have exactly 1-fold Question 9(multiple choice worth 6 points) (05. Which transformations compose the similarity transformation that maps Figure 1 onto Figure 2 Figre 1-R, Dilation go.

Any two pairs of sides are proportional, and the angles included between these sides are congruent: ĪB / A′B′ = BC / B′C′ and ∠ ABC is equal in measure to ∠ A′B′C′.

Which transformations compose the similarity transformation that maps. This is equivalent to saying that one triangle (or its mirror image) is an enlargement of the other. If there are no dilations in the composition, the scale factor is defined to be 1.

All the corresponding sides are proportional: ĪB / A′B′ = BC / B′C′ = AC / A′C′.

If ∠ BAC is equal in measure to ∠ B′A′C′, and ∠ ABC is equal in measure to ∠ A′B′C′, then this implies that ∠ ACB is equal in measure to ∠ A′C′B′ and the triangles are similar.

Any two pairs of congruent angles, which in Euclidean geometry implies that their all three angles are congruent:.

There are several criteria each of which is necessary and sufficient for two triangles to be similar: Due to this theorem, several authors simplify the definition of similar triangles to only require that the corresponding three angles are congruent. Note that the "AAA" is a mnemonic: each one of the three A's refers to an "angle". This is known as the AAA similarity theorem. It can be shown that two triangles having congruent angles ( equiangular triangles) are similar, that is, the corresponding sides can be proved to be proportional. Then, S must be rotated around a center C of degree so that S coincides with S’.

In this lesson you will explore properties of similar polygons and which transformations produce similar figures. If a point X(x, y) is dilated by a factor k, the new location is X'(kx, ky).Two triangles, △ ABC and △ A′B′C′, are similar if and only if corresponding angles have the same measure: this implies that they are similar if and only if the lengths of corresponding sides are proportional. Which transformations compose the similarity transformation that maps S onto S’ Answer: First, dilate S by a scale factor of r > 1 until the corresponding segment lengths are equal in measurement to those of S’. Activity 4.2.1 Similarity Transformations. Trapezoid DEFG is dilated according to the ruleDO,4 (x,y) to form the image trapezoid D'E'F'G', which is shown on the graph. Types of transformation are reflection, rotation, translation and dilation.ĭilation is a type of transformation that enlarges or reduces an object thereby producing an image which has the same shape but a different size as the object. Which composition of similarity transformations maps polygon ABCD to polygon A'B'C'D' a dilation with a scale factor of 1/4 and then a translation.

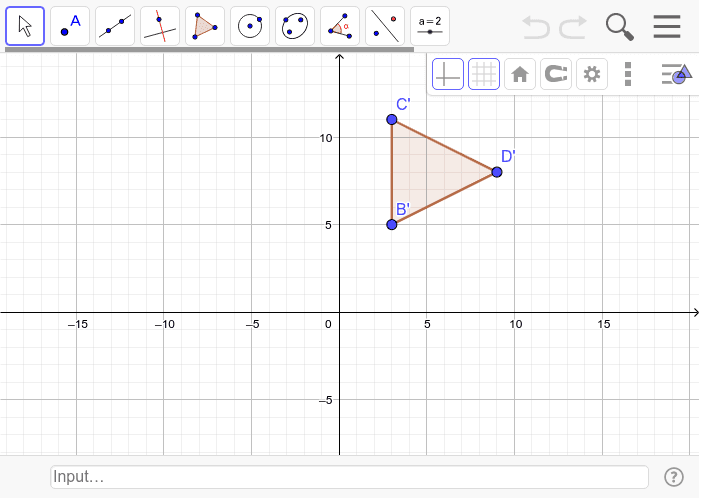
Transformation is the movement of a point from its initial location to a new location. The above example shows that if we want to have an interpolation which corresponds to the intended motion, then we can t systematically use the principal. Now, in the dual space, orthogonal transformations map. Given that the vertices of polygon ABCD are at A(-3, 3), B(5, 3), C(5, -1), D(1, -5) while the vertices of polygon A'B'C'D' are at A'(-5, -2), B'(-3, 2), C'(-3, -3), D(-4, -4) Any similarity transformation of Euclidean space can be obtained as a composition of four basic. A dilation with a scale factor of 4 and then a translation